Converting Decimal to Binary:

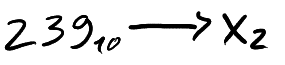
To convert a decimal number to binary, we first need to create a table that represents the binary "bits" corresponding to powers of 2.

Next, identify the smallest number in the table that is larger than or equal to your decimal number. For example, in this case, we are converting 239. The smallest number in the table that fits 239 is 256. This means 256 gets a "0" in the binary result, while 128 gets a "1."

After subtracting 128 from 239, we are left with 111. Now, we need to "build" the number 111 using smaller numbers in the table (64, 32, 16, 8, 4, 2, 1).

Hint: If the decimal number is odd, the rightmost bit in the binary representation will always be "1". For example:

239 is odd, so its binary representation ends with "1":
239 = xxxxxxx1

238 is even, so its binary representation ends with "0":
238 = xxxxxxx0

After "building" 111, we can now fill in the binary bits:

So, 239 in decimal equals 11101111 in binary because:
128 + 64 + 32 + 8 + 4 + 2 + 1 = 239

Additional Notes:

1. Always start counting from zero when creating a binary table:

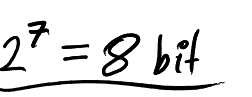
2. The highest representable number for each bit length is one less than the next bit length:

- 8 bits: 255
- 9 bits: 511
- 4 bits: 15

Converting Binary to Decimal:

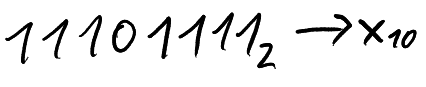
To convert a binary number back to decimal, we once again need to set up a "bit table" representing powers of 2.

Write the binary digits in the table, starting from the rightmost side and moving left. This will help us identify which powers of 2 are included in the sum.

Now, add up the values of the positions where there is a "1". In this case, we have:

128 + 64 + 32 + 8 + 4 + 2 + 1 = 239

Therefore, 11101111 in binary equals 239 in decimal.

Congratulations! You now know how to convert between decimal and binary numbers.